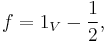Positive and negative parts
In mathematics, the positive part of a real or extended real-valued function is defined by the formula
Intuitively, the graph of 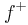 is obtained by taking the graph of
is obtained by taking the graph of  , chopping off the part under the x-axis, and letting
, chopping off the part under the x-axis, and letting 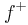 take the value zero there.
take the value zero there.
Similarly, the negative part of f is defined as
Note that both f+ and f− are non-negative functions. A peculiarity of terminology is that the 'negative part' is neither negative nor a part (like the imaginary part of a complex number is neither imaginary nor a part).
The function f can be expressed in terms of f+ and f− as
Also note that
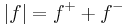 .
.
Using these two equations one may express the positive and negative parts as
Another representation, using the Iverson bracket is
One may define the positive and negative part of any function with values in a linearly ordered group.
Measure-theoretic properties
Given a measurable space (X,Σ), an extended real-valued function f is measurable if and only if its positive and negative parts are. Therefore, if such a function f is measurable, so is its absolute value |f|, being the sum of two measurable functions. The converse, though, does not necessarily hold: for example, taking f as
where V is a Vitali set, it is clear that f is not measurable, but its absolute value is, being a constant function.
The positive part and negative part of a function are used to define the Lebesgue integral for a real-valued function. Analogously to this decomposition of a function, one may decompose a signed measure into positive and negative parts — see the Hahn decomposition theorem.
References
- Jones, Frank (2001). Lebesgue integration on Euclidean space, Rev. ed. Sudbury, Mass.: Jones and Bartlett. ISBN 0763717088.
- Hunter, John K; Nachtergaele, Bruno (2001). Applied analysis. Singapore; River Edge, NJ: World Scientific. ISBN 9810241917.
- Rana, Inder K (2002). An introduction to measure and integration, 2nd ed. Providence, R.I.: American Mathematical Society. ISBN 0821829742.
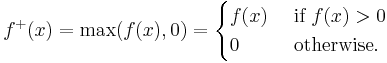
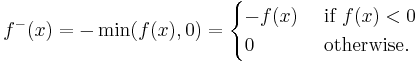
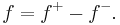
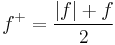
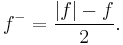
![f^%2B= [f>0]f\,](/2012-wikipedia_en_all_nopic_01_2012/I/39c4f90488d7ee3369328d8046d06469.png)
![f^-= -[f<0]f.\,](/2012-wikipedia_en_all_nopic_01_2012/I/342504eff42158c174d138b7e234a336.png)